2020. 3. 19. 20:36ㆍETC/Algorithm Concept
삽입정렬이란?
삽입정렬(Insert Sort)은 정렬되어 있는 부분집합에 정렬할 새로운 원소의 위치를 찾아 삽입하는 방법이다.
삽입정렬에서 정렬할 자료가 두개가 있다.
먼저 S(Sorted)와 U(United)로 나누어져 있다. 앞부분 원소부터 정렬을 수행하여 정렬된 앞부분의 원소들은 부분집합 S가 되고 아직 정렬되지 않은 나머지 원소들은 부분집합 U가 된다.
정렬되지 않은 부분집합 U의 원소를 하나씩 꺼내서 이미 정렬되어 있는 부분집합 S의 마지막 원소부터 비교하면서 위치를 찾아 삽입하여 부분집합 S의 원소는 하나씩 늘리고 부분집합 U의 원소는 하나씩 줄인다. U의 원소를 모두 삽입하여 공집합이 되면 삽입 정렬이 완성된다.
위의 글처럼 책에서는 삽입정렬의 정의가 기술되어있다. 쉽게 말해서 두개 리스트로 나누어서 정렬되지 않은 원소 하나를 선택해서 정렬된 리스트에 정렬된 상태로 삽입하는 것이다. U는 첫번째 원소를 선택하고 S는 마지막 원소부터 0번째순서로 U의 첫번째 원소랑 비교한다.
list = {5,3,1,2,4}
위처럼 정렬되지 않은 리스트가 있다고 하자. 저 리스트를 정렬해보자

S = 정렬된 리스트
U = 정렬되지 않은 리스트
<Step 1>
U의 첫번째 원소인 3과 S의 마지막 원소 5를 비교한다.
S(5)> U(3)이 크고 더이상 비교할 수 있는 S의 원소가 없기 때문에 3은 5왼쪽에 삽입하면 된다. 결과는 아래처럼 된다.

<Step 2>
U의 첫번째 원소인 1과 S의 마지막 원소인 5와 비교한다. S(5) > U(1) 일때는 그 다음 S 원소와 U의 원소를 비교한다.
여기서는 S의 첫번째 원소인 3과 U의 첫번째 원소인 1하고 비교한다.
S(3) > U(1)이기 때문에 3 왼쪽에 삽입을 하면 된다.

<Step 3>
U의 첫번째 원소인 2와 S의 마지막 원소인 5를 비교한다. S(5) > U(2)이기 때문에 다음 S의 원소 3이랑 비교한다.
S(3)>U(2)이기 때문에 그 다음 S의 원소랑 비교한다. S(1)<U(2)이기 때문에 1 오른쪽에 삽입한다.

<Step 4>
U의 첫번째 원소인 4와 S의 마지막 원소인 5를 비교한다. S(5) > U(4)이기 때문에 그 다음 S의 원소 3이랑 비교한다.
S(3) < U(4)이기 때문에 3 오른쪽에 삽입한다.

그럼 이제 U의 원소는 없고 S의 원소만 남게 된다. 그러면 정렬은 끝이 된다.
빅오는 O(n^2)이 된다. 반복문을 이용해서 계속 비교해나가기 때문이다.
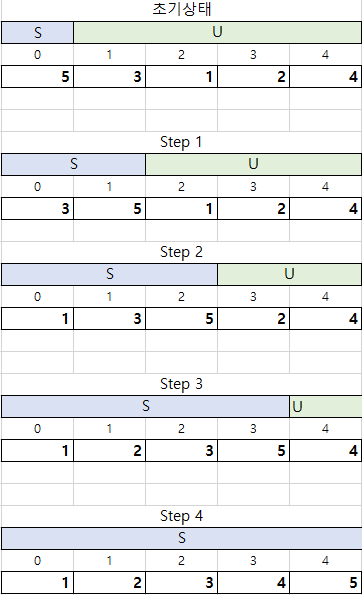
전체적인 step을 보면 밑에 그림과 같다.
<JAVA 소스 >
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | public class Sort { public static void main(String[] args) { int[] a = {5, 3, 4, 7, 2, 8, 6, 9, 1}; int aSize = a.length; for (int i = 1; i < aSize; i++) { int baseNum = a[i]; int baseIndex = i; for (int j = i - 1; j >= 0 ; j--) { //기준 숫자의 앞에서부터 0번째 index까지 검색 if (baseNum < a[j]) { //검색한 숫자가 기준 숫자보다 작으면 교환 int tmp = a[j]; a[j] = a[baseIndex]; a[baseIndex] = tmp; baseIndex = j; } } } //배열 출력 for(int i =0; i<aSize;i++){ System.out.print(a[i]+" "); } System.out.println(); } } | cs |
혹시나 잘못된 정보나 더 좋은 의견 있으면 댓글로 남겨주세요! 언제든지 환영합니다!
'ETC > Algorithm Concept' 카테고리의 다른 글
| Linked List는 무엇인가? (0) | 2024.02.11 |
|---|---|
| Bubble Sort(버블정렬) (0) | 2022.01.25 |
| Kadane 알고리즘 (0) | 2017.07.25 |
| RadixSort 기수 정렬 java (0) | 2017.01.06 |
| 계수 정렬(Counting Sort) java (0) | 2016.12.27 |